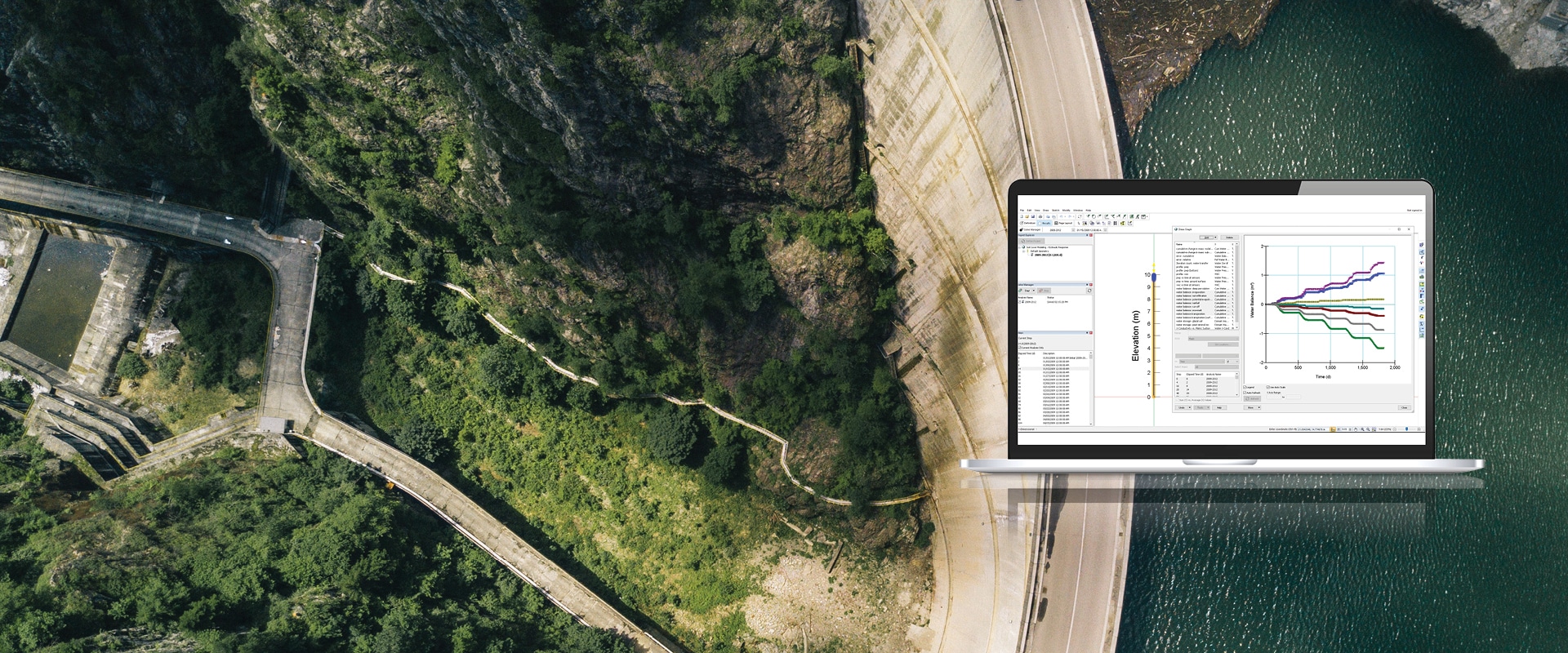
Инженерная геология включает в себя определение геологической и гидрогеологической системы, понимание определяющего поведения породы и моделирование. Все три компонента взаимосвязаны с опытом.
Таким образом, моделирование является неотъемлемой частью практической инженерной геологии. Эта идея была представлена ведущим инженером-строителем Джоном Берландом в его основополагающей лекции Нэша и представлена в «треугольнике Берланда».
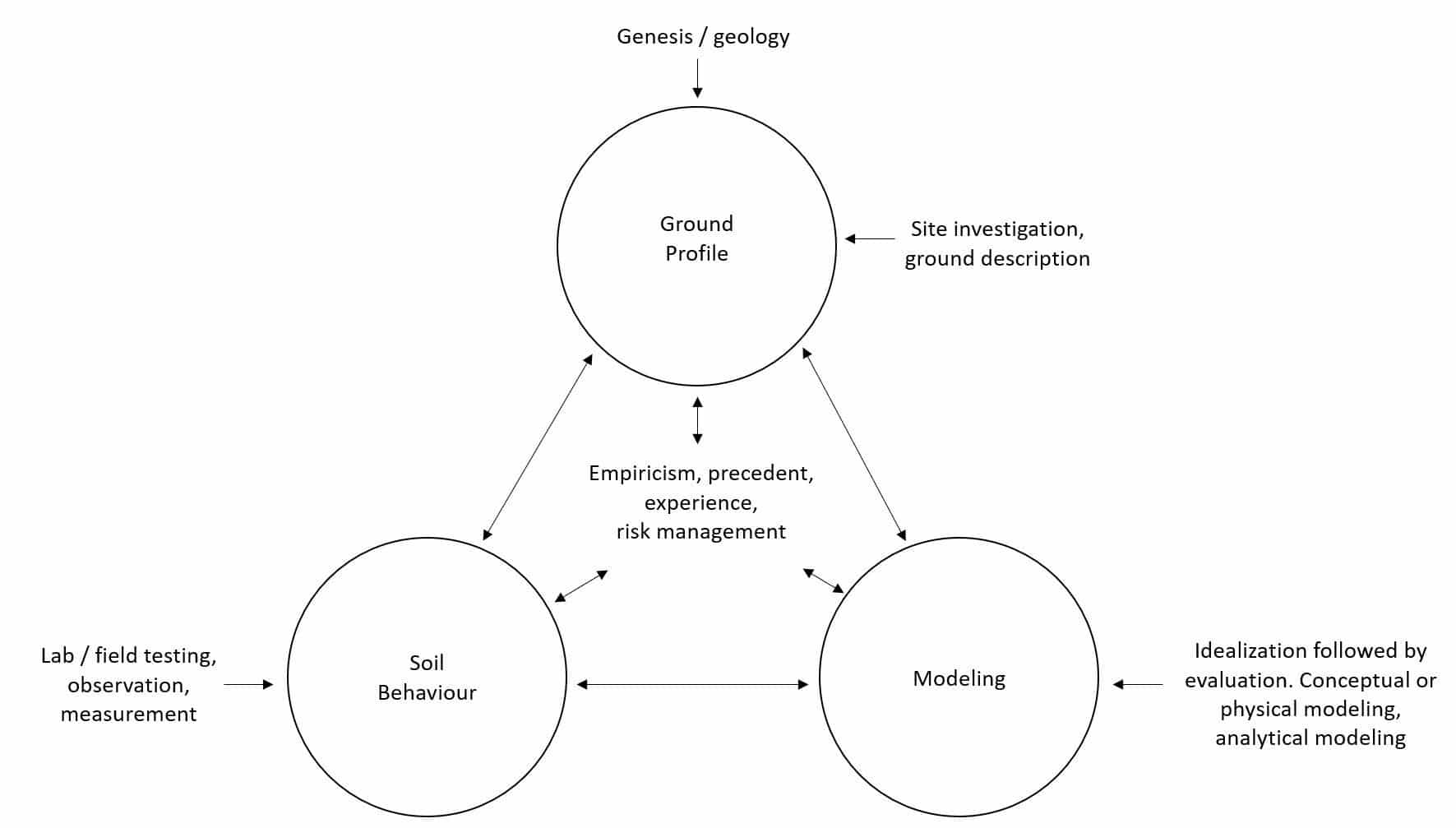
Рисунок 1. Треугольник Берланда (Проектирование наземных объектов, 1996 г.). Из основополагающей лекции Нэша
Идея Берланда была развита Барбуром и Краном (2004 г.), заявившими, что математическая модель — это упрощенное представление сложной реальности, основанное на нашем понимании. Они определили моделирование так:
«процесс, с помощью которого мы извлекаем из сложной физической реальности соответствующую математическую реальность, на которой можем основывать проект. Роль числовой модели состоит в том, чтобы просто помочь нам разработать соответствующую математическую абстракцию.»
Таким образом, выполняя процесс моделирования, инженеры могут получить четкое представление о физической системе и принять более взвешенные решения. Это подтверждает идею о том, что моделирование связано с процессом, а не с прогнозированием, и его наибольшей силой является разработка соответствующей математической абстракции сложной физической системы. Однако максимальная польза может быть достигнута только в том случае, если моделирование включено во весь процесс решения проблемы.
Числовые модели
Анализ методом конечных элементов — это лишь один тип числовой модели, который содержит меньше ограничений и дополняет другие типы числовых моделей, такие как аналитические и графические решения. Его преимущество в том, что он может справиться с такими сложностями, как:
а) сложные геологические и гидрогеологические условия;
б) нетривиальные физические процессы;
в) множественные и конкурирующие альтернативы конструкции и экономические последствия; а также
г) процесс принятия решений, который может быть затруднен необходимостью доведения идей до регулирующих органов и широкой общественности.
Инженерные проблемы, связанные с Землей, особенно сложны, потому что природные системы демонстрируют чрезвычайную пространственную изменчивость, сложное и иногда не поддающееся количественной оценке поведение горных пород, несовместимые временные и пространственные масштабы и во многих случаях физические процессы, которые до конца не изучены. Барбур и Кран (2004 г.) проиллюстрировали это примером из практики, сравнивая различные числовые модели с измеренными смещениями оснащенной опорными конструкциями подпорной стены для глубокой выемки. Ни один из прогнозов боковых смещений не был точным и не соответствовал измерениям.
Является прогноз надежным?
Частично неточность их предсказаний была связана со сложностями, ошибками концептуализации, а частично — с численными задачами. Это приводит к выводу, что предсказать точный отклик невозможно, поскольку даже в самой точной математической модели невозможно воспроизвести все детали, присутствующие в физической задаче. Подтверждает ли это, что предсказание не должно быть основной целью числового моделирования?
В предыдущей практике общие схемы физического поведения по факту были адекватно смоделированы, и потому численные решения обеспечили соответствующую основу для проектирования.
В чем ключевое преимущество числового моделирования?
Ли Барбур (Lee Barbour) из GeoStudio говорит: «На самом деле, процесс числового моделирования улучшает инженерную оценку и обеспечивает основу для понимания сложных физических процессов. Это итеративный процесс моделирования, и он включает в себя основные этапы.»
Четыре основных этапа моделирования
- Определить цель моделирования и разработать концептуальную модель проблемы
- Определить соответствующие теоретические модели (например, физических процессов), описывающие ключевые физические свойства
процессы - Разработать математическое описание этих процессов и убедиться, что оно дает точное решение.
- Интерпретировать результаты по отношению к наблюдаемой физической реальности
1. Определить цель моделирования и разработать концептуальную модель
Это самые важные этапы процесса, и именно здесь числовое моделирование может быть исключительно полезным, поскольку процесс заставляет нас включать информацию о геологии и гидрогеологии участка, лабораторные данные и любую другую соответствующую информацию (например, последовательность строительства) в концептуальную модель проблемы. Концептуальная модель также должна быть связана с целями моделирования.
2. Определить соответствующую теоретическую модель
Это включает в себя понимание лежащей в основе физики и определяющего поведения, управляющего характеристиками пород. С нашей точки зрения, это означает, что формулировка числовой модели репрезентативна для исследуемого физического процесса. Это понимание проявляется в разработке модели через определение граничных условий и свойств пород. Эти компоненты часто меняются по мере того, как мы повторяем процесс моделирования; уточнение модели по мере развития понимания физической системы и появления дополнительных полевых и лабораторных данных.
3. Разработать математическое описание этих процессов и проверить точность
В конце концов, концептуальные и теоретические модели приводят к математическому решению. При анализе методом конечных элементов вычерчивается геометрия проблемного домена, определяются свойства породы, и к домену применяются граничные условия. Проверка решения выполняется, чтобы обеспечить сходимость, соответствующую пространственную и временную дискретизацию и правильное применение физических свойств (возможно, путем сравнения с аналитическим решением). Эта «мантра» от простого к сложному гарантирует, что мы будем уверены в численном решении.
4. Интерпретировать результаты по отношению к наблюдаемой физической реальности
Наконец, результаты интерпретируются в контексте физической реальности. Являются ли результаты оправданными? Результаты анализа методом конечных элементов можно сравнивать с данными полевого мониторинга, и их всегда следует интерпретировать в свете информации, использованной для разработки концептуальных и теоретических моделей.
Ли пришел к выводу, что «числовые модели развиваются в ходе процесса моделирования, поскольку нам сложно интерпретировать результаты. Это может означать увеличение сложности концептуальной модели; однако построение гипотез с высокими степенями сложности при отсутствии подтверждающих наблюдений не только проблематично, но и усложняет оставшиеся части процесса или делает их невозможными. Лучшие числовые модели содержат ровно столько сложности, чтобы математическая абстракция могла разумно приблизиться к физической реальности.»
Справочная информация
С.Л. Барбур и Дж. Кран, 2004 г. Числовое моделирование: Прогноз или процесс? Геотехнические новости, декабрь: 44-52.
Берланд Дж.Б., 1987 г. Лекция Нэша: Обучение механике сыпучих тел — личный взгляд. Протоколы 9-й Европейской конференции по механике грунтов и фундаментостроению. Дублин, том. 3, стр. 1427-1447.