O novo formato do modelo de sub-blocos do Leapfrog, baseado na subdivisão de octree, melhora a representação da geometria na modelagem em blocos.
Agora, o Leapfrog tem um novo formato do modelo de sub-blocos baseado na subdivisão de octree, que garante uma representação muito mais eficiente da geometria na modelagem em blocos. Neste blog, explicamos os princípios básicos desse novo formato e o que isso significa para a modelagem em blocos.
Então, o que é uma octree? Vamos começar com a definição da Wikipédia.
“Uma octree é uma estrutura de dados em árvore na qual cada nó interno tem oito filhos. As octrees são mais usadas para subdividir recursivamente um espaço tridimensional em oito octantes.
(Fonte: Wikipedia https://en.wikipedia.org/wiki/Octree)
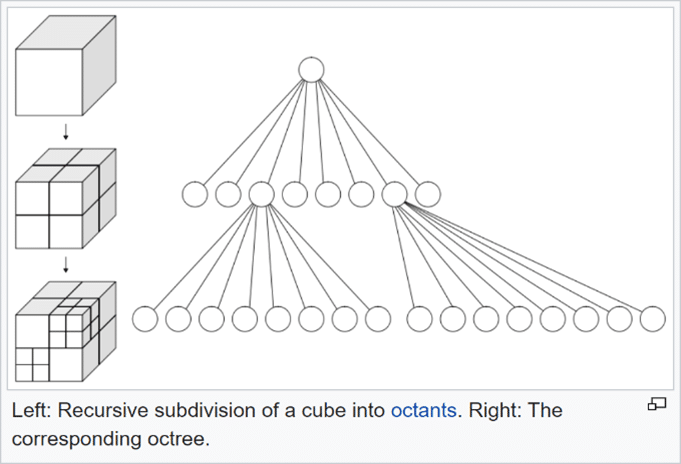
Cada repetição corresponde a uma subdivisão binária das dimensões de um bloco pai (ou sub-bloco criado anteriormente). Em nossa implementação de octree, são permitidos até seis níveis de repetição binária abaixo do nível do bloco pai com o menor sub-bloco criado sendo, portanto, 1/64º (=1/2^6) da dimensão da célula pai. Modificamos nossa implementação para que diferentes níveis de repetição possam ser aplicados a cada eixo. Se seis níveis de repetição forem aplicados a todos os três eixos, o volume do menor sub-bloco criado será, portanto, 0,0003815% do pai (=1/(1/64)^3) e, teoricamente, até 262.144 (=64^3) sub-blocos podem ser criados por pai. Na prática, nada perto dessa quantidade de sub-blocos é criada, pois a divisão de blocos ou sub-blocos só é gerada se um limite passar por eles.
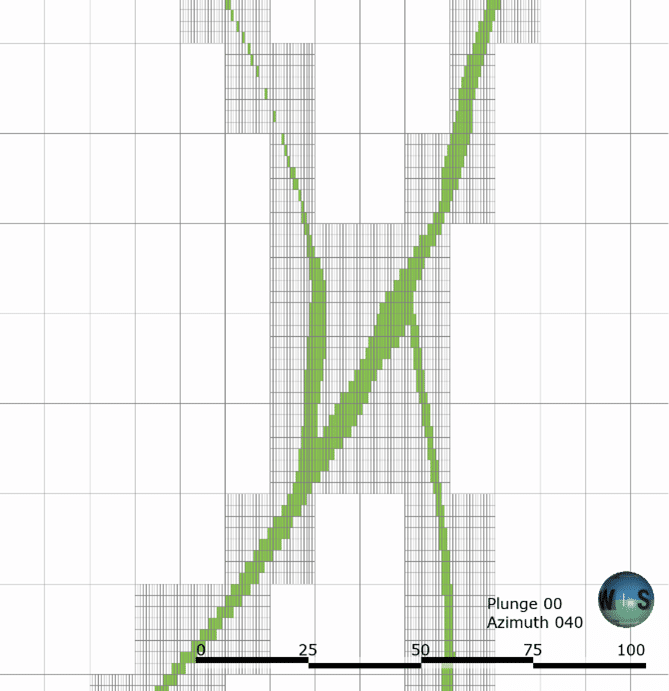
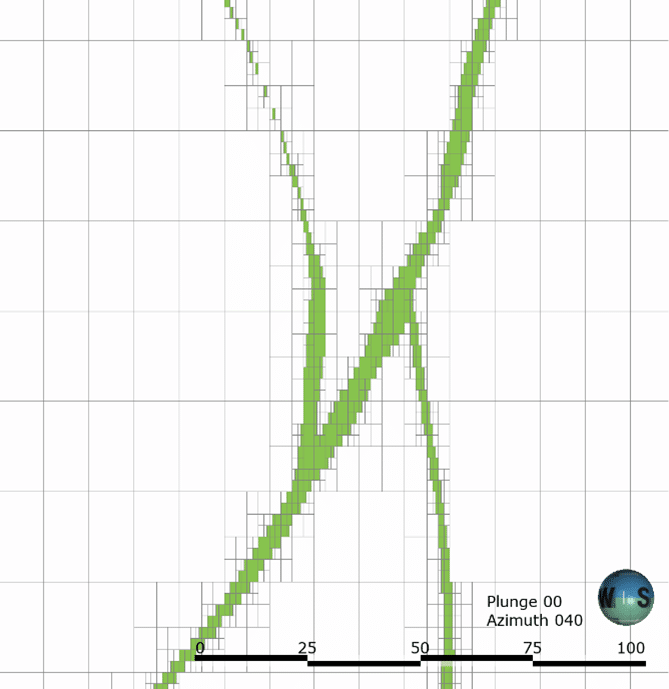
Ilustração de geometrias de sub-blocos criadas pelo antigo formato composto apenas por sub-blocos do Leapfrog (à esquerda) e pelo novo formato de octree (à direita).
A redução exata da quantidade de sub-blocos depende da geometria e do número de blocos gerados e varia em cada projeto.
Como exemplo, a tabela abaixo compara o número de sub-blocos necessários para representar um sistema de veios estreitos contendo quatro veios usando o atual formato de sub-blocos do Leapfrog e o novo formato de octree. De maneira geral, o modelo de octree requer apenas 15% dos blocos exigidos pelo antigo modelo composto apenas por sub-blocos. Para o sistema de veios, a redução é menor (55% do anterior) porque os veios são muito finos e são, na maioria das vezes, representados pelo menor sub-bloco. Para geometrias de domínios mais volumosos, a redução proporcional será maior, geralmente é necessário apenas 25% do anterior (ou seja, uma redução de 75%).
| Sub-bloco atual | Sub-bloco de octree | ||
| Ponto base: | 250, 2070, 1180 | 250, 2070, 1180 | |
| Dimensão limite | 1040, 290, 600 | 1040, 290, 600 | |
| Dimensão do bloco pai | 20,10,20 | 20,10,20 | |
| Dimensão em blocos | 52, 29, 30 | 52, 29, 30 | |
| Sub-blocos | 8,16,8 | 8,16,8 | |
| Azimute/mergulho | 310°/0° | 310°/0° | |
| Número total de blocos pai: | 45,240 | 45,240 | |
| Após a geração | |||
| Número de blocos pai divididos | 6469 (14.3%) | 6173 (13.6%) | |
| Pais 20, 10, 20 | 38,771 | 39,067 | |
| Sub-bloco = 10, 5, 10 | 25,259 | ||
| Sub-bloco = 5, 2,5, 5 | 103,340 | ||
| Sub-bloco = 2,5, 1,25, 2,5 | 619,361 | ||
| Sub-bloco = 2,5, 0,625, 2,5 | 6,624,256 | 195,838 | % do anterior |
| Total de todos os blocos/sub-blocos | 6,663,027 | 982,865 | 15% |
| Sistema de veios apenas com blocos | 404,082 | 224,008 | 55% |
Assim, é possível gerar arquivos de tamanhos menores quando os modelos de blocos do Leapfrog são exportados e agilizar o processamento devido ao menor número de células. Além disso, o tamanho dos projetos nos levou a escolher a octree como base para o nosso novo modelo. Sabemos que a octree não é o formato de sub-blocos mais eficiente em termos de redução do número de células, mas a estrutura hierárquica de uma octree é muito eficiente e traz grandes vantagens para o armazenamento e a recuperação de informações de blocos, além de permitir uma visualização mais rápida.
Para o modelo de veios mostrado acima, o modelo antigo de sub-blocos requer 1,548 Gb de espaço em disco enquanto o novo formato de octree requer apenas 18 Mb. O tamanho desse projeto em particular foi bastante reduzido, de 1,74 Gb para 210 Mb.
O trabalho para otimizar ainda mais o tamanho e o desempenho dos modelos de octree é contínuo.
Todas as ferramentas padrão de validação e geração de relatórios disponíveis com os modelos de sub-blocos também estão disponíveis com o formato de octree; são elas: cálculos e filtros, relatórios estatísticos, relatórios resumo, curvas de tonelagem x teor e gráficos de faixas (swath).
É “correto do ponto de vista geoestatístico” estimar diretamente com base em sub-blocos? Essa questão, que surge frequentemente com modelos de sub-blocos, é ainda mais relevante quando os sub-blocos são de vários tamanhos. Essa é uma questão muito ampla para ser explorada aqui; portanto, será discutida futuramente em um artigo do blog. Entretanto, basta dizer que a implementação da nossa estimativa com base em sub-blocos aborda todas as considerações sobre “suporte” ao transferir uma malha de discretização adequada ao pai em cada sub-bloco. Isso garante que a correção de suporte decorrente da krigagem de blocos seja apropriada às dimensões do bloco pai.
O caminho de upgrade para conversão dos seus modelos de blocos existentes é simples; basta criar um novo modelo e escolher os objetos a serem gerados e avaliados. Você pode exportar cálculos e filtros e importá-los novamente para o novo modelo. Será necessário recriar relatórios e criar gráficos de faixas (swath). Como esse processo é muito fácil, decidimos não criar um upgrade automatizado. Ao recriar o modelo, você pode avaliar e comparar os modelos antigos e novos lado a lado; é uma validação adicional importante. Acreditamos que você perceberá imediatamente as vantagens que o nosso novo modelo oferece e fará essa migração.
Se a opção variável Z for necessária (e você não puder usar a subdivisão refinada em um eixo para alcançar a resolução geométrica que essa opção permite), é possível continuar usando o modelo de sub-blocos atual.
Importação de modelos de sub-blocos
Após outra implementação muito aguardada, agora é possível importar um modelo de sub-blocos de octree no formato .csv para o Leapfrog, o que permite visualizar, validar e gerar relatórios de modelos importados. Você pode adicionar novos desencadeamentos, avaliações e estimativas aos modelos importados preservando a integridade das categorias e dos valores importados.
É importante observar que os modelos importados devem estar de acordo com a regra que estabelece a dimensão mínima do sub-bloco como uma subdivisão binária da dimensão da célula pai (em x, y e z). Os blocos com dimensões arbitrárias de sub-blocos podem ser processados desde que cumpram essa regra. Na prática, muitos modeladores definem seus modelos arbitrários dentro dessa restrição geométrica, pois facilita a transferência de modelos de blocos entre diferentes aplicativos.
Veja na Figura 2 como a interface de importação segue o padrão conhecido para escolher um arquivo de entrada e selecionar as colunas a serem importadas antes de definir a estrutura da malha a ser importada como dimensões pai e do sub-bloco, posição e extensão.
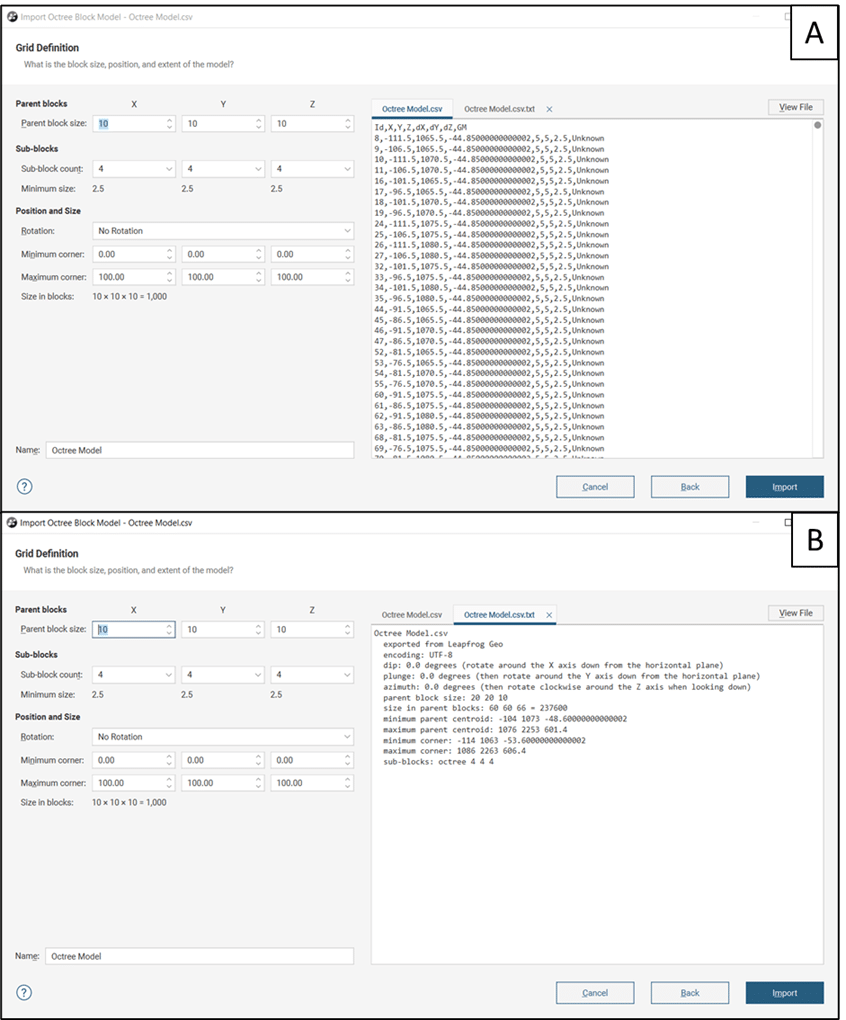
Figura 2. A interface de importação para o novo formato do modelo de sub-blocos segue o padrão conhecido para escolher um arquivo de entrada e selecionar as colunas a serem importadas e, em seguida, definir a malha (dimensões pai e do sub-bloco, posição e extensão). (A) mostra o conteúdo do arquivo .csv; (B) mostra a definição de malha.
Para modelos não rotacionados, especificar as posições de canto mínimo e máximo nas coordenadas ortogonais do projeto é uma tarefa simples.
Se o modelo for rotacionado, atualmente duas opções predefinidas estão disponíveis para importar arquivos .csv específicos exportados do Leapfrog e do Surpac. Essas duas opções estão configuradas para aceitar os mínimos, os máximos e as rotações de modelos conforme as informações do cabeçalho que podem (e devem) ser exportadas com os arquivos de dados.
Os modelos exportados de outros pacotes (em que as convenções de rotação podem ser distintas) ainda podem ser importados usando uma dessas opções. Se você souber as dimensões do modelo, use a opção do Surpac para especificar os cantos máximos como canto mínimo mais dimensões do modelo (ou seja, no espaço de pré-rotação). Recomendamos primeiro importar o modelo como pontos, filtrar os pontos para isolar os blocos pai e, em seguida, usar esses pontos para verificar se o modelo que os contém está corretamente localizado em relação aos locais dos dados.
Sabemos que a experiência de importação de modelos rotacionados ainda não está otimizada. O trabalho para refinar e melhorar o recurso de importação está em andamento.
Resumo das vantagens do novo formato do modelo de sub-blocos
Confira abaixo o resumo das principais vantagens ao usar o nosso novo formato do modelo de sub-blocos com ramificação de octree:
- Melhoria da representação da geometria na modelagem em blocos sem gerar arquivos de modelo de blocos difíceis de controlar.
- Menos blocos e menos linhas, portanto, arquivos menores de modelo de blocos.
- Arquivos menores de modelo de blocos e projetos do Leapfrog mais leves para exportação ou publicação de dados no Central.
- Menos blocos e estimativas mais rápidas.
”Continuamos investindo intensamente no Leapfrog. Ao implantar esse novo formato do modelo de sub-blocos com subdivisão de octree, os usuários podem melhorar a representação geométrica de domínios de estimativa e modelos geológicos com um modelo de blocos mais leve, rápido e eficiente.
Mike Stewart, Technical Doman Expert at Seequent




