Tipos de modelos para la inversión de datos TEM/FEM en Aarhus Workbench

Muchas inversiones se realizan solo con modelos uniformes, pero muchas veces la resolución es lo suficientemente buena como para percibir cambios más abruptos en la geología que los que permite el modelo uniforme. Debido a ello, el uso de inversiones posteriores con modelos de capas puede ser interesante para obtener información complementaria sobre el subsuelo. Analizaremos los modelos por capas, los modelos en bloque y los modelos brevemente agudos, así como la opción de crear modelos individuales por capas a partir de modelos uniformes existentes.

Generalidades

[00:00:02.320]
<v ->Hola, gracias por participar en esta presentación.</v>

[00:00:05.650]
Soy Bjarke Roth y soy geofísico

[00:00:07.910]
con Aarhus GeoSoftware.

[00:00:10.191]
Hoy vamos a analizar los tipos de modelos,

[00:00:12.000]
ya que los utilizamos para realizar las inversiones en Aarhus Workbench.

[00:00:15.970]
Digamos que hemos medido algunos datos,

[00:00:18.040]
Podría ser que se hicieran mediciones TDEM, como esta,

[00:00:21.090]
a partir de un sistema EM de dominio temporal aerotransportado,

[00:00:23.350]
o podría tratarse de un sistema EM en el dominio de la frecuencia.

[00:00:28.060]
Nos esforzamos por eliminar los acoplamientos

[00:00:30.740]
y el ruido de los datos

[00:00:32.368]
para que no solo reflejen la geología.

[00:00:35.900]
Antes de poder darlo a conocer,

[00:00:37.030]
tenemos que transformarlo en un modelo físico del subsuelo

[00:00:40.290]
que luego un geólogo pueda utilizar

[00:00:41.530]
para crear los modelos más sofisticados con los que trabaja.

[00:00:45.450]
Desafortunadamente, no hay una forma directa de hacerlo.

[00:00:48.440]
Y, de hecho,

[00:00:49.273]
resulta mucho más fácil hacerlo de otra manera.

[00:00:52.570]
Conocemos la física y con una descripción precisa del sistema

[00:00:57.320]
es posible calcular la respuesta anticipada.

[00:00:59.040]
que se mediría para un modelo determinado.

[00:01:01.330]
Por lo tanto, lo que podemos hacer es comparar esta respuesta directa

[00:01:04.450]
con los datos medidos.

[00:01:07.000]
Hacemos esta comparación con una función objetivo,

[00:01:09.360]
un ejemplo de ello es este residuo de datos.

[00:01:12.260]
Comparamos los datos observados y los datos previstos

[00:01:14.870]
y los normalizamos con la incertidumbre de los datos.

[00:01:17.220]
En realidad, la C aquí son las entradas diagonales

[00:01:19.610]
de la matriz de covarianza,

[00:01:20.760]
pero contiene la incertidumbre de los datos al cuadrado.

[00:01:23.590]
Un valor de uno

[00:01:24.423]
significa que los datos se ajustaron al ruido.

[00:01:26.680]
Todo lo que esté por debajo de uno es, en ese sentido, igualmente correcto.

[00:01:30.060]
Un valor igual a dos

[00:01:31.100]
significa que los datos se ajustaron

[00:01:32.527]
con un intervalo de dos veces al ruido y así sucesivamente.

[00:01:35.568]
Si minimizamos esta función,

[00:01:36.510]
encontraremos la versión de nuestro modelo

[00:01:38.740]
que más se acerque a los datos que observamos.

[00:01:43.480]
El modelo 1D más sencillo que podemos obtener es un modelo de medio espacio,

[00:01:46.950]
es decir, un modelo con un solo parámetro de resistividad

[00:01:49.210]
para describir el subsuelo.

[00:01:51.510]
Así que vamos a dar un vistazo rápido y algo simplificado

[00:01:53.770]
en cómo funciona el proceso de inversión para esta situación.

[00:01:57.698]
Si pudiéramos calcular el residuo de los datos

[00:02:00.040]
de todos los valores residuales permitidos, se vería así,

[00:02:03.550]
pero la inversión no puede visualizar esta curva.

[00:02:06.434]
En su lugar, en cada iteración,

[00:02:08.700]
se calculará el residuo de los datos

[00:02:11.620]
y, luego, la derivada del parámetro del modelo.

[00:02:14.910]
Más adelante, puede ajustar el parámetro del modelo de resistividad

[00:02:17.550]
basándose en esa derivada dando un salto al subespacio.

[00:02:21.580]
Esto se repite una y otra vez

[00:02:25.970]
hasta que ya no se puede mejorar el resultado.

[00:02:30.160]
Es de esperar que termine en el mínimo global

[00:02:34.660]
y no en un mínimo local.

[00:02:38.470]
Este enfoque se denomina algoritmo de Levenberg-Marquardt

[00:02:41.120]
o de mínimos cuadrados amortiguados.

[00:02:42.820]
Incluí algunas referencias,

[00:02:44.300]
para quien esté interesado en ellos.

[00:02:47.040]
No siempre se encuentra un mínimo global,

[00:02:48.780]
pero resulta bastante sólido cuando las funciones tienen un buen comportamiento

[00:02:51.240]
y los parámetros de partida son razonables.

[00:02:53.480]
En la mayoría de los casos,

[00:02:54.313]
las funciones con las que trabajamos tienen un comportamiento bastante bueno.

[00:02:57.410]
Sin embargo, en algunos casos se puede llegar a situaciones

[00:03:00.710]
en las que hay que mejorar el modelo de partida

[00:03:02.670]
para no acabar en un mínimo local.

[00:03:05.839]
Por supuesto, por lo general queremos un poco más de detalle

[00:03:08.450]
en nuestros modelos 1D que solo el parámetro de resistividad.

[00:03:12.180]
Desde el punto de vista conceptual, el modelo más sencillo es el de capas,

[00:03:14.410]
en el que tenemos unas cuantas capas,

[00:03:16.050]
cada una de las cuales tiene una resistividad y un grosor.

[00:03:19.000]
Por desgracia, no es el tipo de modelo más fácil de trabajar.

[00:03:22.480]
Las capas que se obtienen

[00:03:23.520]
no siempre se corresponden directamente

[00:03:25.240]
con las capas geológicas generales,

[00:03:27.250]
por lo que se necesita práctica y conocimiento del subsuelo

[00:03:29.730]
para hacerlo bien.

[00:03:31.130]
Pero, en breve, hablaremos de por qué es así.

[00:03:34.820]
En cambio,

[00:03:35.653]
pasaremos al modelo uniforme como punto de partida.

[00:03:39.120]
Tenemos más capas, de 20 a 40 dependiendo del tipo de datos,

[00:03:43.040]
pero solo se estiman las resistividades.

[00:03:45.470]
El espesor se mantiene fijo

[00:03:46.770]
con un tamaño creciente con la profundidad.

[00:03:48.720]
Además, las resistividades también son verticales

[00:03:50.670]
para garantizar la continuidad entre las capas,

[00:03:53.000]
de ahí el nombre de uniforme.

[00:03:55.760]
Analicemos esto un poco.

[00:03:57.453]
Hay una gran ventaja en este enfoque.

[00:04:00.230]
Las condiciones de inicio son mucho menos importantes

[00:04:02.940]
que en los modelos de capas.

[00:04:05.850]
Claro que tenemos las resistividades de partida

[00:04:07.440]
de todas estas capas,

[00:04:08.950]
pero casi siempre utilizamos un modelo de partida uniforme

[00:04:11.990]
para no introducir estructura en el modelo con resistividades.

[00:04:14.630]
Y, mientras, no nos alejemos demasiado.

[00:04:16.750]
A partir de donde tenemos que llegar con las resistividades,

[00:04:19.050]
esto solo se traducirá

[00:04:20.400]
en tiempos de inversión un poco más largos,

[00:04:22.980]
ya que para cambiar las resistividades la inversión

[00:04:25.770]
necesita unas cuantas iteraciones adicionales y tenemos algunas opciones

[00:04:29.930]
para mejorar ese modelo de partida,

[00:04:32.227]
esas resistividades de partida.

[00:04:34.580]
Sobre todo, como las capas están fijas,

[00:04:36.970]
la configuración de las capas no es tan importante para el modelo definitivo,

[00:04:40.870]
el modelo uniforme final, como lo es para un modelo por capas.

[00:04:46.663]
Lo único que tenemos que decidir para la configuración

[00:04:48.590]
es el límite de la primera capa, el límite de la última capa,

[00:04:50.590]
el número de capas y las restricciones verticales,

[00:04:53.430]
que podemos hacer de forma relativamente objetiva,

[00:04:55.610]
basándonos en el instrumento utilizado y el tipo de datos.

[00:04:58.960]
La resolución esperada cerca de la superficie

[00:05:00.468]
nos da el límite de la primera capa,

[00:05:02.950]
si la hacemos demasiado fina,

[00:05:04.300]
solo estará determinada por el valor inicial

[00:05:06.720]
y las restricciones.

[00:05:08.680]
La mayor profundidad de penetración esperada

[00:05:11.100]
nos da el límite de la última capa,

[00:05:13.170]
de nuevo, si la hacemos muy profunda,

[00:05:14.900]
solo estará determinada por el valor inicial

[00:05:17.010]
y las restricciones.

[00:05:18.140]
Y eso lo podemos solucionar

[00:05:19.640]
sin medida de profundidad de investigación más adelante.

[00:05:23.090]
Pero si no se profundiza lo suficiente,

[00:05:25.813]
no podremos ajustar los datos del último trimestre.

[00:05:30.050]
La resolución esperada nos da una idea sobre el número de capas a utilizar,

[00:05:33.500]
esto también se relaciona con las restricciones verticales.

[00:05:37.660]
Sirven para estabilizar la inversión

[00:05:39.940]
y reducir los efectos de sobreimpulso y subimpulso

[00:05:41.850]
que, de otro modo, podríamos ver con capas mal resueltas.

[00:05:44.850]
No obstante, esto puede establecerse de forma relativa y objetiva

[00:05:47.550]
en función de la variación geológica prevista.

[00:05:50.486]
entonces, es simplemente una cuestión de introducir los números.

[00:05:52.680]
en una calculadora de discretización del modelo

[00:05:55.020]
y dejar que distribuya las capas

[00:05:56.810]
para que el aumento de la discretización de espesor

[00:06:00.940]
vaya hacia abajo por el modelo.

[00:06:04.770]
Hablé de las restricciones,

[00:06:06.304]
pero no expliqué realmente lo que son.

[00:06:09.070]
Todas nuestras restricciones sirven de factores.

[00:06:10.930]
Un valor de dos significa que a la resistividad de la capa superior

[00:06:13.810]
o inferior se le permite un intervalo sigma en su resistividad

[00:06:17.340]
que va desde la capa de resistividad dividida por dos

[00:06:19.840]
hasta la capa de resistividad multiplicada por dos.

[00:06:22.070]
Así que no es un límite estricto,

[00:06:23.280]
En principio puede cambiar más rápido,

[00:06:25.713]
pero será más costoso para la inversión hacerlo.

[00:06:30.890]
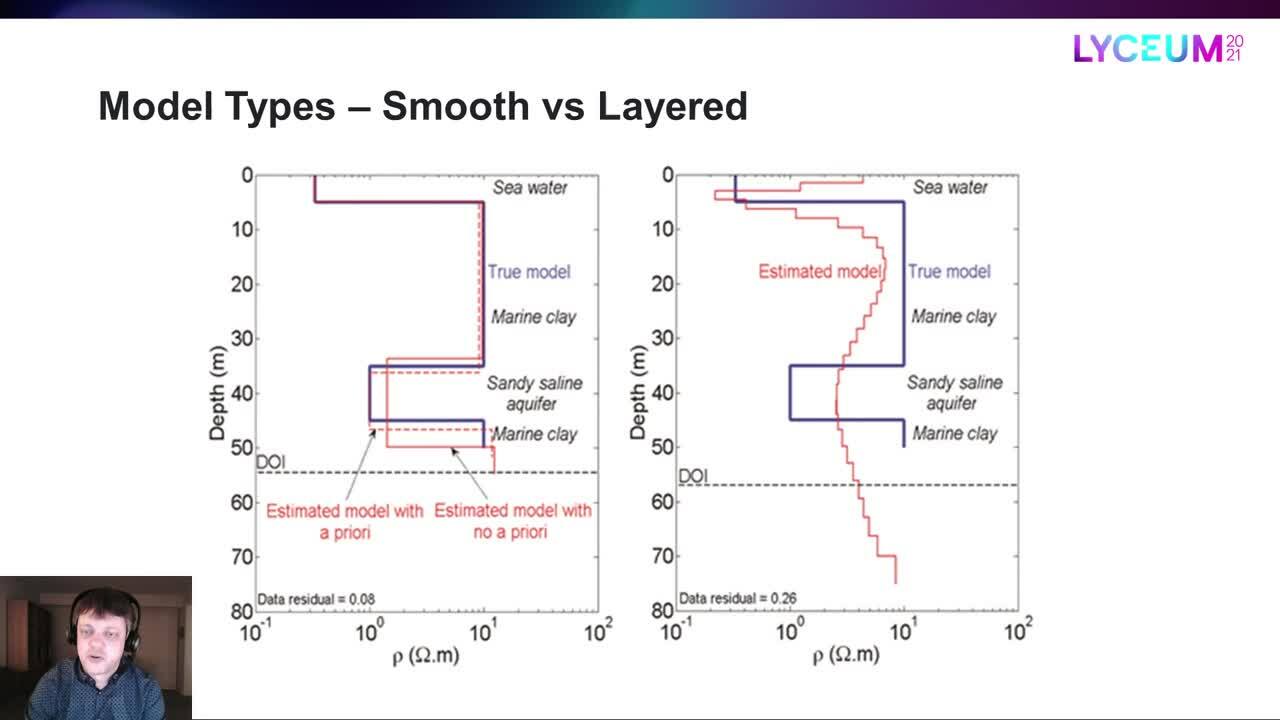
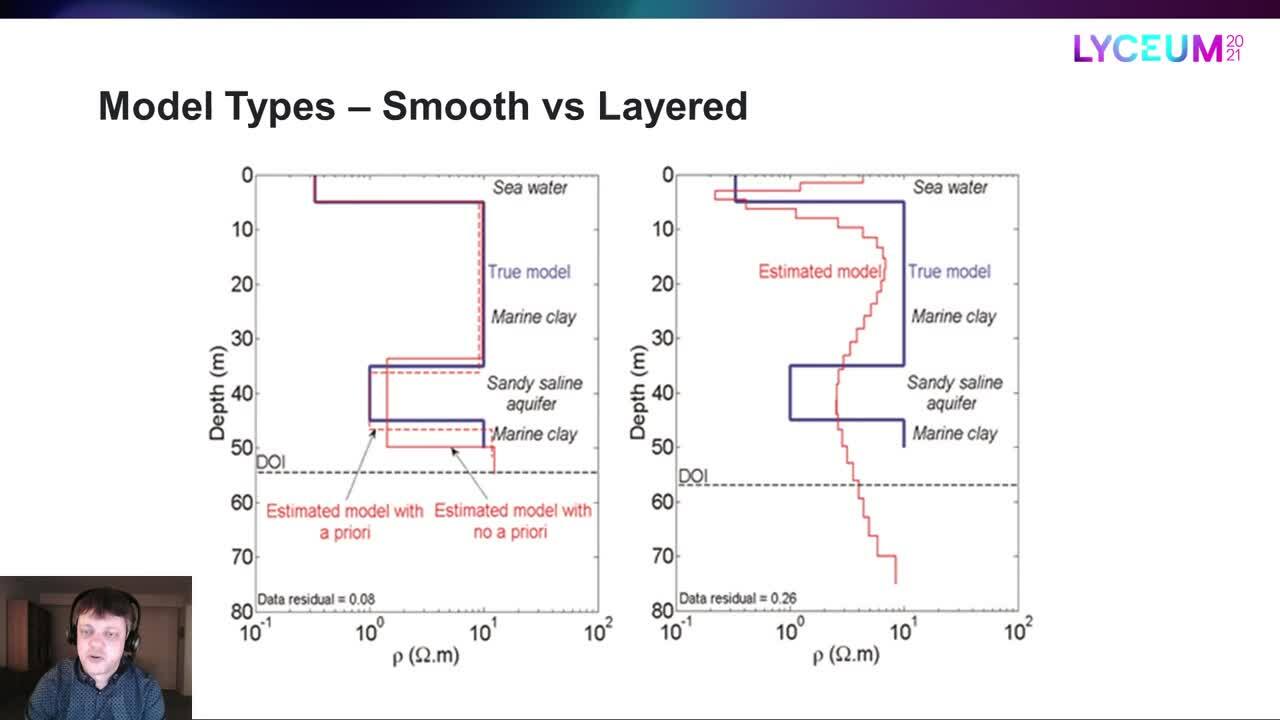
Veamos un ejemplo.

[00:06:32.980]
La línea azul es el modelo verdadero,

[00:06:34.470]
mientras que la línea roja es el modelo uniforme estimado.

[00:06:37.340]
El DOI es la profundidad de la investigación

[00:06:39.770]
que mencioné brevemente antes,

[00:06:41.390]
que es la profundidad hasta la que podemos confiar en que los resultados

[00:06:44.130]
dependan principalmente de los datos

[00:06:45.920]
y no de los valores de partida y las restricciones.

[00:06:49.300]
Por lo tanto, el tipo de modelo uniforme reprodujo la estructura general

[00:06:53.149]
pero no obtenemos exactamente las transiciones de capa correctas

[00:06:56.160]
y las resistividades de las capas aquí.

[00:06:59.730]
Vamos a compararlo con la estimación del modelo de capas.

[00:07:03.240]
En este caso tenemos dos modelos de capas,

[00:07:05.800]
uno sin antecedentes

[00:07:07.010]
y otro en el que se utilizó la resistividad de la tercera capa

[00:07:08.840]
para ayudar a la inversión en la dirección correcta.

[00:07:13.290]
Está claro que el modelo de capas

[00:07:15.230]
puede mejorar las transiciones y las resistividades de las capas,

[00:07:18.360]
sobre todo si le ayudamos.

[00:07:22.640]
Sin embargo, si iniciamos la inversión con espesores de capa

[00:07:25.360]
demasiado alejados,

[00:07:26.640]
puede acabar colocando las transiciones de capa de forma diferente.

[00:07:29.340]
y desperdiciamos capas donde realmente no las necesitamos.

[00:07:32.220]
Esta situación puede mejorarse

[00:07:33.670]
con el conocimiento de la estructura global

[00:07:35.470]
que podemos obtener del modelo uniforme,

[00:07:37.200]
pero puede ser necesario hacer varios intentos para conseguirlo.

[00:07:40.717]
Es posible utilizar el enfoque

[00:07:42.960]
de los límites de la primera y la última capa

[00:07:44.829]
o editar las capas por separado,

[00:07:47.060]
pero esto tiende a ser más de prueba y error

[00:07:49.300]
que la configuración del modelo uniforme,

[00:07:51.440]
tal vez porque el modelo por capas,

[00:07:52.650]
más que un modelo uniforme,

[00:07:53.940]
refleja la natividad de sus datos.

[00:07:56.190]
Asegúrense de centrar sus esfuerzos de configuración en la parte superior

[00:08:00.300]
del modelo, donde se reflejará la mayor parte

[00:08:02.340]
de la natividad de sus datos.

[00:08:05.150]
Por lo tanto, si observamos estos dos tipos de modelos,

[00:08:06.940]
Nos quedamos con que “todos los modelos son erróneos, algunos son útiles”.

[00:08:10.600]
ninguno de ellos tiene todas las respuestas,

[00:08:12.750]
pero ambos modelos ofrecen una visión útil

[00:08:14.810]
y, en cierto modo, complementaria sobre el subsuelo.

[00:08:20.317]
Ahora vamos a ampliar un poco el enfoque

[00:08:22.540]
antes de ver los dos últimos tipos de modelos.

[00:08:25.250]
Muchas veces hacemos la inversión de muchos modelos al mismo tiempo,

[00:08:27.550]
con lo cual, por supuesto, tenemos que hablar

[00:08:29.400]
de cómo entran en juego las restricciones laterales.

[00:08:31.229]
Se espera una cierta continuidad en la geología.

[00:08:34.638]
Dependerá de la geología específica, claro,

[00:08:37.610]
pero se espera que los modelos próximos

[00:08:39.670]
tengan algunas similitudes

[00:08:41.960]
Podemos establecer restricciones siguiendo la línea de vuelo,

[00:08:45.480]
lo que se denomina inversión lateral restringida o LCI.

[00:08:48.894]
O bien, podemos establecer restricciones sobre las líneas de vuelo

[00:08:51.030]
y entre las líneas de vuelo,

[00:08:52.280]
lo que se denomina inversión espacialmente restringida o SCI.

[00:08:55.680]
Las dos son todavía inversiones en 1D,

[00:08:58.040]
el cálculo de avance aquí todavía se hace en 1D.

[00:09:01.710]
Pero los modelos se vuelven cuasi 2D para LCI y cuasi 3D para SCI.

[00:09:07.920]
En la práctica,

[00:09:08.760]
las restricciones del LIC serán algo así.

[00:09:12.013]
Los puntos rojos son las posiciones del modelo

[00:09:13.860]
y las líneas negras son las restricciones.

[00:09:16.380]
Las restricciones se determinan con un algoritmo,

[00:09:18.070]
que garantiza que obtengamos una estructura como esta,

[00:09:20.950]
donde siempre tenemos restricciones en las líneas de vuelo,

[00:09:23.310]
así como en las líneas de vuelo cercanas.

[00:09:26.300]
Hay que destacar que,

[00:09:27.770]
a diferencia de lo que ocurre con las restricciones verticales,

[00:09:29.910]
en este caso hay que tener en cuenta la distancia.

[00:09:32.490]
No queremos que las restricciones sean igual de estrictas

[00:09:34.320]
entre todas las posiciones del modelo.

[00:09:36.640]
Establecemos entonces una distancia de referencia para nuestra inversión.

[00:09:39.950]
Todas las restricciones entre los modelos

[00:09:41.760]
que se mantienen dentro de esa distancia, utilizan el hecho como cierto,

[00:09:46.270]
mientras que los modelos más alejados

[00:09:47.740]
tendrán esa restricción a escala para ser más débil.

[00:09:51.290]
Si establecemos esta distancia de referencia

[00:09:52.710]
igual a la distancia media de sondeo entre nuestros modelos

[00:09:55.400]
por la línea de vuelo,

[00:09:56.750]
la restricción lateral puede establecerse

[00:09:58.650]
en función de la cantidad esperada de variación geológica

[00:10:01.490]
en la zona, en lugar de ser un factor arbitrario.

[00:10:05.100]
El cálculo se encargará, entonces, del resto de nosotros.

[00:10:08.350]
Con algunos tipos de datos,

[00:10:09.210]
esta distancia de referencia se calcula automáticamente,

[00:10:11.770]
pero, en otros casos, forma parte de la configuración del modelo.

[00:10:15.580]
También se restringe algo como la altitud,

[00:10:18.440]
pero esas restricciones se mantienen separadas

[00:10:20.090]
y solo se restringen a lo largo de las líneas de vuelo.

[00:10:25.480]
Ahora podemos unir todas las piezas.

[00:10:27.920]
Cuando hablábamos antes de la inversión,

[00:10:29.830]
utilizábamos una función objetivo sencilla

[00:10:31.570]
que solo tenía en cuenta los datos residuales.

[00:10:33.930]
La función objetivo completa,

[00:10:35.200]
por supuesto, también tiene en cuenta las restricciones

[00:10:37.520]
y los antecedentes.

[00:10:39.850]
Así como en el residuo de los datos se comparan los datos observados y los datos futuros

[00:10:45.229]
normalizados con la incertidumbre de los datos,

[00:10:47.390]
en las partes de las restricciones

[00:10:48.990]
se comparan los parámetros del modelo de restricciones

[00:10:54.656]
normalizados con el factor

[00:10:56.095]
establecido para la fuerza de esas restricciones.

[00:10:59.296]
Y en la parte de los valores a priori se comparan los parámetros del modelo

[00:11:01.551]
con los valores a priori para esos parámetros

[00:11:03.903]
del modelo normalizados con los factores

[00:11:05.610]
establecidos para la fuerza de esos valores a priori.

[00:11:09.310]
La parte de las restricciones es la más interesante aquí,

[00:11:11.430]
ya que pone de manifiesto algunas diferencias entre los modelos

[00:11:14.370]
de capas y los uniformes.

[00:11:16.190]
Hay restricciones verticales en las resistividades,

[00:11:18.000]
pero solo para los modelos uniformes.

[00:11:19.430]
Hay restricciones laterales en las resistividades,

[00:11:21.389]
esto lo usan tanto los modelos de capas como los uniformes.

[00:11:24.320]
También disponemos de una restricción lateral en el espesor de la capa

[00:11:26.120]
de todas las profundidades de la capa, pero solo para los modelos de capas.

[00:11:30.240]
Tanto el enfoque del grosor

[00:11:31.073]
como el de la profundidad para el modelo de capas funciona,

[00:11:33.090]
pero hay, por supuesto, algunas diferencias en la configuración

[00:11:35.930]
cuando utilizamos factores sobre la profundidad de todas las capas anteriores

[00:11:39.130]
en lugar de solo el grosor de las capas individuales

[00:11:43.130]
que se detalla.

[00:11:44.990]
La parte de las restricciones también es interesante

[00:11:47.030]
porque es la base de los dos últimos tipos de modelos.

[00:11:52.120]
La idea con ambos es tener un modelo

[00:11:54.880]
que se configura de forma similar a como se configura un modelo uniforme,

[00:11:58.306]
sin necesidad de saber mucho

[00:12:00.150]
sobre dónde deben estar las transiciones de las capas,

[00:12:02.710]
sino que el resultado final

[00:12:03.950]
adquiere más las características del resultado del diseño

[00:12:06.730]
con las capas más diferenciadas.

[00:12:10.790]
El método por excelencia se denomina modelo de bloques

[00:12:13.040]
y es realmente sorprendente por su sencillez.

[00:12:16.030]
En lugar de utilizar la diferencia al cuadrado,

[00:12:20.067]
se utiliza la diferencia absoluta para la parte de las restricciones.

[00:12:24.720]
Tengo un gráfico del costo de la penalización de los términos de la suma aquí.

[00:12:27.257]
Lo que vemos es la penalización

[00:12:30.217]
dada la diferencia absoluta de los parámetros del modelo

[00:12:33.730]
normalizado con los datos que establecimos

[00:12:35.930]
para las restricciones.

[00:12:37.640]
Es evidente que aquí hay dos regiones.

[00:12:39.370]
Cuando estamos arriba de uno

[00:12:42.710]
el modelo de bloques tiene una penalización mucho menor.

[00:12:47.740]
En este sentido, puede permitir cambios de modelo mucho mayores

[00:12:51.260]
que el modelo uniforme.

[00:12:54.920]
Cuando estamos por debajo de uno,

[00:12:55.910]
el modelo de bloques tiene una penalización ligeramente mayor,

[00:12:58.980]
por lo que puede, en ese sentido,

[00:13:00.330]
no permitir cambios tan grandes o pequeños como el modelo uniforme.

[00:13:05.090]
Y eso es exactamente lo que vemos.

[00:13:06.780]
En este caso tenemos un modelo uniforme, un modelo de bloques

[00:13:09.607]
y un resultado de inversión de un modelo de capas,

[00:13:12.160]
todos con el mismo sondeo.

[00:13:13.577]
El modelo de bloques cambia más,

[00:13:17.250]
cambia la resistividad con más rapidez

[00:13:20.120]
y se mantiene más estable una vez que se ha producido ese cambio

[00:13:24.500]
que el modelo uniforme.

[00:13:28.270]
La configuración es exactamente la misma que la del modelo uniforme,

[00:13:30.749]
pero el resultado es un poco más parecido

[00:13:33.930]
al del modelo por capas.

[00:13:36.890]
De hecho, la configuración es tan parecida a la del modelo uniforme

[00:13:39.440]
que podemos utilizar una copia de este, un modelo uniforme SCI,

[00:13:43.750]
y simplemente activar un interruptor para invertirlo como un modelo de bloques.

[00:13:50.270]
Los tenemos aquí, no solo para un solo modelo,

[00:13:53.380]
sino en una línea con 3,2 kilómetros de datos SkyTEM.

[00:13:57.700]
En el modelo por capas hay algunos problemas

[00:14:00.140]
en las transiciones,

[00:14:02.530]
pero por lo demás los resultados son bastante buenos

[00:14:04.790]
en todos los tipos de modelos.

[00:14:09.300]
Este último enfoque se denomina modelo agudo.

[00:14:12.690]
Como se puede ver, para esto se complica un poco más,

[00:14:16.810]
No trataré de explicar todos los detalles,

[00:14:20.980]
volví a graficar los costos de penalización de los términos de la suma,

[00:14:25.394]
o al menos la mayor parte de ella,

[00:14:26.970]
ya que es probable que ignore el valor beta aquí.

[00:14:32.090]
Esta vez la penalización se mantiene más cerca de la curva uniforme

[00:14:39.220]
para valores pequeños, pero se desvanece para valores más grandes.

[00:14:43.630]
Una vez que se llega a uno o más,

[00:14:46.490]
se convierte en el número de variaciones

[00:14:48.810]
en lugar de la cantidad total de variación

[00:14:51.090]
que se agrega al costo de la penalización.

[00:14:55.530]
Este enfoque se denomina “soporte de gradiente mínimo”.

[00:14:59.320]
En la práctica, se obtiene un conjunto de parámetros de agudeza,

[00:15:03.200]
uno con agudeza vertical

[00:15:04.520]
y otro con agudeza lateral.

[00:15:06.620]
Estos están relacionados con este valor beta que omití.

[00:15:09.394]
Influyen en el número de bloques que se obtienen.

[00:15:11.808]
Aunque se utilizan para las restricciones verticales y laterales,

[00:15:15.260]
Afectan a la cantidad de variación dentro de los bloques.

[00:15:18.060]
Sin embargo, el número de bloques depende más bien de los datos,

[00:15:20.410]
por lo que es más bien como si establecieras,

[00:15:21.808]
de lo diferentes que deben ser los bloques

[00:15:24.040]
que de su número real.

[00:15:26.177]
Veamos algunos resultados.

[00:15:29.220]
Según la configuración,

[00:15:30.320]
el resultado puede pasar de ser muy similar a un modelo uniforme

[00:15:34.340]
a algo como esto,

[00:15:35.599]
donde acaba siendo bastante parecido al modelo por capas.

[00:15:39.330]
Se puede cambiar las resistividades muy rápidamente,

[00:15:41.873]
pero, por supuesto, sigue estando limitado por la resolución

[00:15:46.100]
de las capas fijas que le asignamos.

[00:15:50.580]
En este sentido, es igual que el modelo uniforme,

[00:15:53.530]
pero sin duda puede acercarse más al modelo por capas

[00:15:55.950]
en el resultado.

[00:15:57.400]
Es necesario acostumbrarse a él.

[00:15:59.050]
Los valores numéricos de los parámetros de agudeza

[00:16:01.210]
son algo diferentes a los de las restricciones,

[00:16:03.540]
pero hay sugerencias de valores utilizables en la Wiki de F1,

[00:16:06.970]
que se puede abrir desde Aarhus Workbench.

[00:16:09.670]
Gracias a los valores laterales, los bloques se distinguen mejor.

[00:16:12.657]
Si bien las restricciones verticales y laterales

[00:16:14.840]
habituales requieren valores numéricos más pequeños

[00:16:16.940]
de lo que estamos acostumbrados,

[00:16:18.381]
los ajustes previos de Aarhus Workbench permiten

[00:16:21.070]
tener en cuenta esta circunstancia,

[00:16:23.030]
pero por lo demás se comportan exactamente como se esperaba.

[00:16:27.120]
Los valores más grandes permitirán una mayor variación

[00:16:29.400]
dentro de cada uno de los bloques.

[00:16:34.200]
El resultado que tenemos aquí se encontró utilizando la configuración predeterminada,

[00:16:39.320]
así que no se desanimen demasiado,

[00:16:41.140]
debido a la cantidad en la que esto puede ajustarse.

[00:16:46.120]
Aquí están de nuevo no solo para el modelo único

[00:16:49.210]
sino en una línea con 3,2 kilómetros de datos SkyTEM.

[00:16:54.550]
En algunas áreas,

[00:16:55.677]
el modelo agudo parece ser mejor

[00:16:59.530]
que el resultado de capas,

[00:17:00.970]
y este era un resultado de capas bastante bueno.

[00:17:04.750]
Para resumir los tipos de modelos,

[00:17:05.985]
se comienza con una inversión del modelo uniforme.

[00:17:08.580]
Si se desea fijar el límite de una capa específica,

[00:17:11.987]
los modelos por capas son la mejor opción,

[00:17:15.710]
ya que con ellos se pueden mover realmente las capas,

[00:17:19.290]
pero cuanto más complicada es la geología,

[00:17:21.316]
más difícil resulta hacerlo.

[00:17:23.860]
Si está satisfecho con el modelo uniforme,

[00:17:25.270]
pero desea una versión más discreta,

[00:17:27.640]
tiene las opciones en bloque y aguda.

[00:17:30.060]
Los bloques utilizan exactamente la misma configuración que los modelos uniformes.

[00:17:32.690]
es muy fácil intentarlo.

[00:17:34.460]
Los modelos agudos utilizan la misma configuración de base que los modelos uniformes,

[00:17:37.180]
excepto por los parámetros agudos agregados

[00:17:39.720]
y las restricciones verticales y laterales,

[00:17:42.520]
a las que puede llevar un tiempo acostumbrarse.

[00:17:45.100]
Sin embargo, puede valer la pena el esfuerzo,

[00:17:46.640]
ya que se obtienen unos resultados muy buenos.

[00:17:49.970]
Eso es todo lo que tengo para ustedes hoy.

[00:17:53.060]
Gracias por su tiempo y que tengan un bonito día.