El nuevo formato del modelo de sub-bloques de Leapfrog, basado en la subdivisión octree, mejorará su representación geométrica al modelar bloques.
Ahora, Leapfrog tiene un formato de modelo de bloques secundarios totalmente renovado basado en la subdivisión octree, que permite una representación geométrica mucho más eficaz en el modelado de bloques. En este blog, explicamos los fundamentos de este nuevo formato y lo que representa para su modelado de bloques.
¿Qué es un octree? Comencemos con la definición de Wikipedia.
“Un octree es una estructura de datos ramificada en la que cada nodo interno tiene exactamente ocho elementos secundarios. Los octrees se utilizan más que nada para dividir un espacio tridimensional mediante una subdivisión recursiva en ocho octantes”.
(Fuente: Wikipedia https://es.wikipedia.org/wiki/Octree)
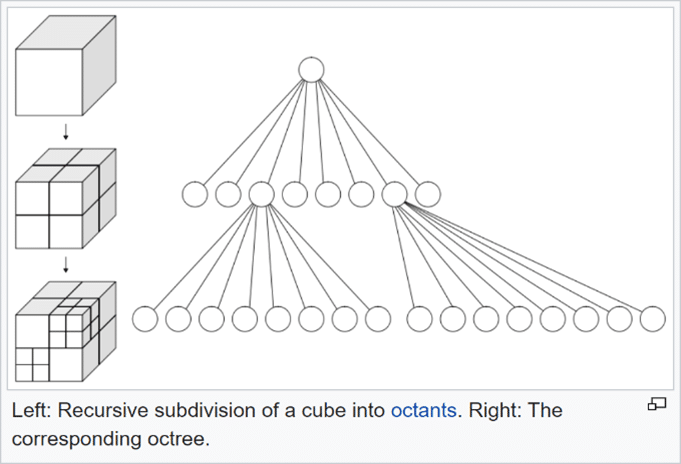
Cada recursión corresponde a una subdivisión binaria de las dimensiones de un bloque principal (o bloque secundario creado anteriormente). En nuestra implementación de octree, se permiten hasta 6 niveles de recursión binaria debajo del nivel del bloque principal; por lo tanto, el bloque secundario más pequeño que puede crearse es de 1/64 (=1/2^6) de la dimensión de la celda principal. Modificamos nuestra implementación para que puedan aplicarse diferentes niveles de recursión en cada eje. Si se aplican 6 niveles de recursión a los tres ejes, el volumen del bloque secundario más pequeño creado es del 0,0003815 % del bloque principal (=1/(1/64)^3) y, en teoría, podrían crearse hasta 262 144 bloques secundarios (=64^3) por cada bloque principal. En la práctica, no se produce esta cantidad de bloques secundarios, porque la división de bloques o bloques secundarios solo se activa si los atraviesa un límite.
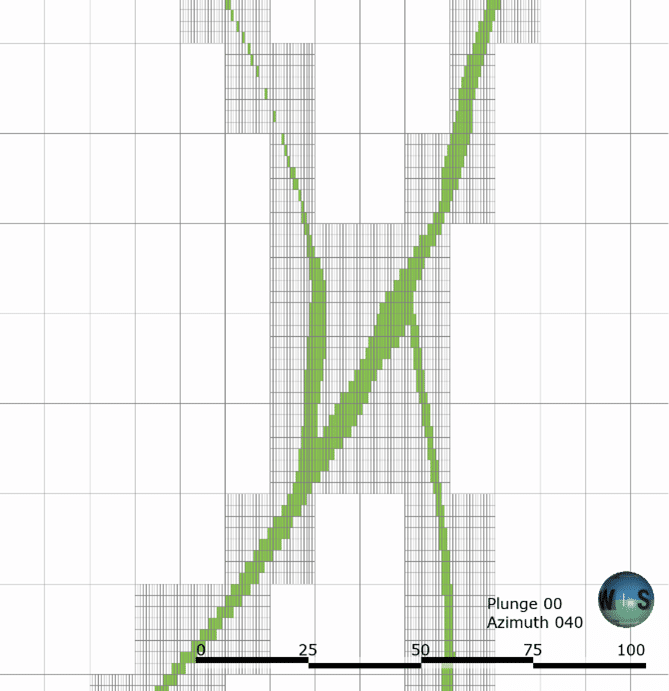
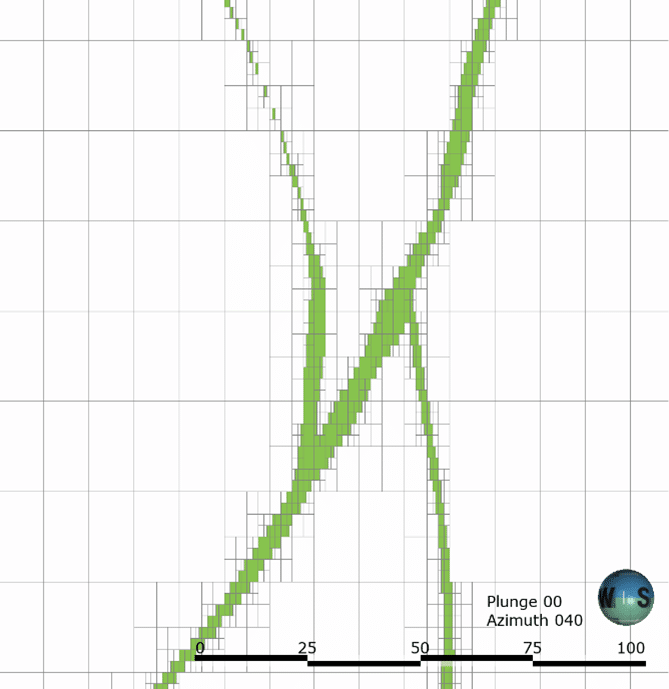
Ilustración de las geometrías de sub-bloques producidas por el anterior formato de sub-bloques de Leapfrog (izquierda) y el nuevo formato de octree (derecha).
La reducción exacta de la cantidad de sub-bloques depende de la geometría y de la cantidad de bloques activados, y variará según el proyecto.
A modo de ejemplo, en la siguiente tabla se compara la cantidad de bloques secundarios necesarios para representar un sistema de vetas estrechas que contiene 4 vetas utilizando el formato de bloques secundarios de Leapfrog existente y el nuevo formato de octree. En general, el modelo octree solo requiere el 15 % de los bloques que necesitaba el anterior modelo completamente formado por bloques secundarios. En el sistema de vetas, la reducción es menor (55 % de la anterior), porque las vetas son muy finas y, en su mayoría, están representadas por el bloque secundario más pequeño. En las geometrías de dominio más grandes, la reducción proporcional será superior; por lo general, solo requerirá un 25 % de la anterior (lo que equivale a una reducción del 75 %).
| Sub-bloque existente | Sub-bloque octree | ||
| Punto base: | 250, 2070, 1180 | 250, 2070, 1180 | |
| Tamaño de límite | 1040, 290, 600 | 1040, 290, 600 | |
| Tamaño de bloque principal | 20,10,20 | 20,10,20 | |
| Tamaño en bloques | 52, 29, 30 | 52, 29, 30 | |
| Sub-bloques | 8,16,8 | 8,16,8 | |
| Azimut/buzamiento | 310°/0° | 310°/0° | |
| Cantidad total de bloques principales: | 45,240 | 45,240 | |
| Después de la activación | |||
| Cantidad de divisiones de bloques principales | 6469 (14.3%) | 6173 (13.6%) | |
| Bloques principales 20,10,20 | 38,771 | 39,067 | |
| Sub-bloque = 10,5,10 | 25,259 | ||
| Sub-bloque = 5,2.5,5 | 103,340 | ||
| Sub-bloque = 2.5,1.25,2.5 | 619,361 | ||
| Sub-bloque = 2.5,0.625,2.5 | 6,624,256 | 195,838 | % del anterior |
| Total de bloques/bloques secundarios | 6,663,027 | 982,865 | 15% |
| Solo bloques del sistema de vetas | 404,082 | 224,008 | 55% |
Esto se traduce en tamaños de archivo más reducidos cuando se exportan los modelos de bloques de Leapfrog y tiempos de procesamiento más rápidos con menos celdas para procesar. Es más, al observar el tamaño del proyecto, se destaca la razón principal por la que elegimos octree como base para nuestro nuevo modelo. Se sabe muy bien que octree no es el formato de bloques secundarios más eficiente en relación con la reducción de la cantidad de celdas, pero la estructura jerárquica de un octree es muy eficiente y ofrece importantes ventajas para el almacenamiento y la recuperación de la información de los bloques, además de una visualización más rápida.
Para el modelo de vetas que se muestra arriba, el anterior modelo de bloques secundarios requiere 1548 GB de almacenamiento en el disco, mientras que el nuevo octree solo requiere 18 MB. El tamaño de este proyecto en particular se reduce de forma considerable de 1,74 GB a 210 MB.
Por el momento, estamos trabajando para optimizar incluso más el tamaño y el rendimiento de los modelos octree.
No es necesario decir que todas las herramientas de validación y presentación de informes estándar que utiliza con los modelos de bloques secundarios existentes también están disponibles en octree: cálculos y filtros, informes estadísticos, informes de resumen, curvas de tonelaje de ley y gráficos de líneas.
Una pregunta que surge con frecuencia con respecto a los modelos de bloques secundarios es si es “geoestadísticamente correcto” estimar de forma directa en los bloques secundarios, algo que es incluso más relevante cuando los bloques secundarios tienen diferentes tamaños. Este es un tema demasiado amplio como para analizarlo aquí y se describirá en otro artículo del blog. Pero basta con decir que nuestra implementación de la estimación en bloques secundarios aborda cualquier inquietud sobre el “soporte”, puesto que transfiere una grilla de discretización apropiada al bloque principal en cada bloque secundario, lo que garantiza que esa corrección de soporte implícita mediante el uso del método de “<em>kriging</em> en bloques” sea apropiada para las dimensiones del bloque principal.
Los pasos para actualizar la conversión de sus modelos de bloques existentes son simples: tan solo cree un modelo nuevo y elija los objetos que quiere activar y evaluar. Puede exportar cálculos y filtros, y volver a importarlos al modelo nuevo. Tendrá que volver a crear los informes y los gráficos de líneas. Este proceso es tan sencillo que decidimos no intentar una actualización para automatizarlo. Volver a crear el modelo le permite evaluar y comparar los modelos anteriores y nuevos en paralelo, una validación adicional de gran valor. Estamos seguros de que comprenderá de inmediato las ventajas que ofrece nuestro nuevo modelo y de que implementará esa migración.
Si necesita la opción Z variable (y no puede utilizar la subdivisión fina en un eje para lograr la resolución geométrica que ofrece), tan solo siga utilizando el modelo de bloques secundarios existente.
Importar un modelo de sub-bloques
También desarrollamos una función muy esperada: ahora podrá importar un modelo de bloque secundario octree en formato CSV a Leapfrog, lo que le permitirá visualizar, validar e informar a partir de modelos importados. Podrá agregar nuevas activaciones y nuevas evaluaciones y estimaciones a los modelos importados a la vez que preservará la integridad de las categorías y los valores importados.
Es importante destacar que los modelos importados deben respetar la regla que define que la dimensión mínima del bloque secundario debe ser una subdivisión binaria de la dimensión de la celda principal (en X, Y y Z). Los bloques con dimensiones arbitrarias de bloques secundarios pueden procesarse siempre y cuando cumplan con esta regla. De cualquier modo, en la práctica, muchos modeladores definen sus modelos arbitrarios con esta restricción geométrica, puesto que facilita la transferencia de los modelos de bloques entre diferentes aplicaciones.
Consulte la Figura 2: se muestra la forma en que la interfaz para importar sigue el patrón habitual de elegir un archivo de entrada y seleccionar las columnas que desea importar antes de definir la estructura de la grilla en la que se importarán los datos: tamaños de bloques principales y secundarios, posición y extensión.
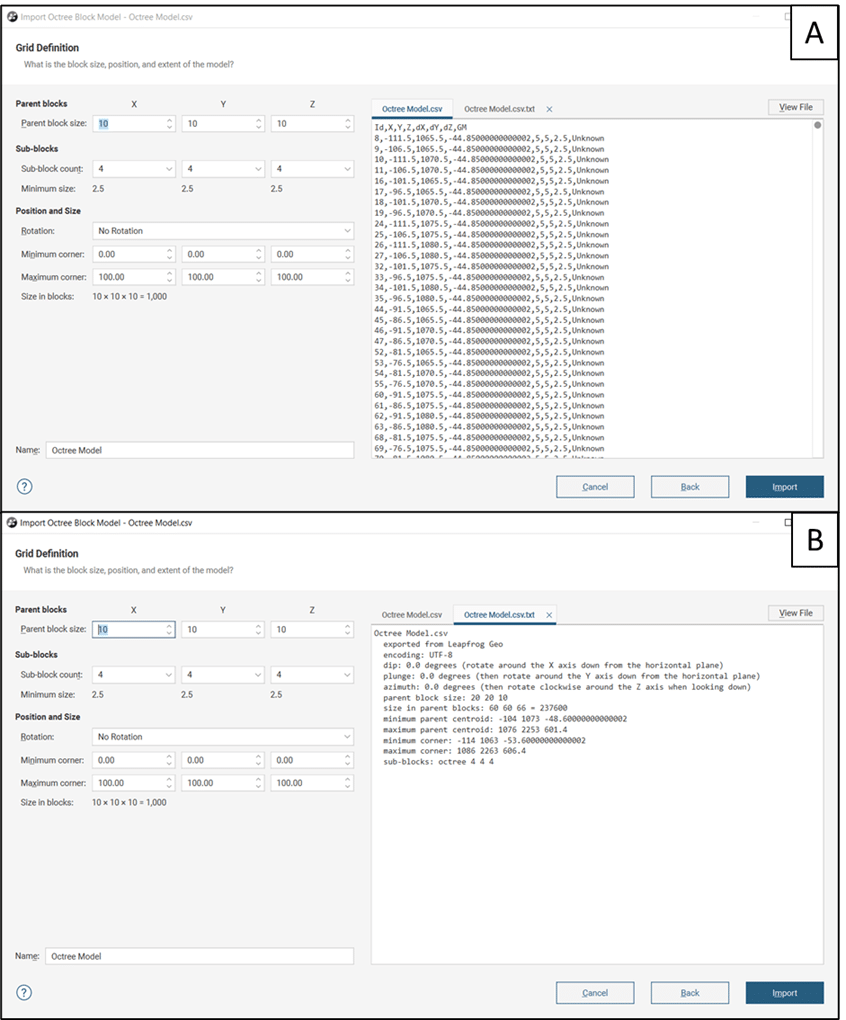
Figura 2. La interfaz para importar el nuevo formato de modelo de bloques secundarios respeta el patrón habitual de elegir un archivo de entrada, seleccionar las columnas que desea importar y, por último, definir la grilla: tamaños de bloques principales y secundarios, posición y extensión. (A) muestra el contenido del archivo csv; (B) muestra la definición de la grilla.
Para los modelos que no giran, es muy fácil especificar las posiciones de esquina mínima y máxima en las coordenadas de proyecto ortogonales.
Si se gira el modelo, por el momento ofrecemos dos opciones predefinidas para importar exportaciones de archivos CSV específicos de Leapfrog y Surpac. Ambas opciones están configuradas para aceptar los valores mínimos, los valores máximos y las rotaciones del modelo, tal como se determina en la información del encabezado que puede (y debe) exportarse con los archivos de datos.
Los modelos exportados desde otros paquetes (en los que pueden diferir las convenciones de rotación) todavía pueden importarse con una de estas opciones. Si conoce las dimensiones del modelo, utilice la opción Surpac para especificar las esquinas máximas como esquina mínima y las dimensiones del modelo (es decir, en el espacio previo a la rotación). Recomendamos importar primero el modelo como puntos, filtrar los puntos para aislar los bloques principales y, luego, utilizar estos puntos para verificar que el modelo contenedor esté correctamente ubicado respecto de las ubicaciones de los datos.
Sabemos que la experiencia de importar modelos girados todavía no está optimizada. Por el momento, estamos trabajando para perfeccionar y mejorar el importador.
Resumen de las ventajas del nuevo formato de modelo de bloques secundarios
En resumen, a continuación indicamos las principales ventajas de utilizar nuestro nuevo formato de modelo de bloques secundarios con la ramificación octree:
- Mejore su representación geométrica en el modelado de bloques sin generar archivos de modelos de bloques difíciles de procesar.
- Se generan menos bloques y menos filas; por lo tanto, los archivos de modelos de bloques son más pequeños.
- Al generarse archivos de modelos de bloques más pequeños, es más fácil exportar o publicar proyectos de Leapfrog en Central.
- Al haber menos bloques, la estimación es más rápida.
”Seguimos invirtiendo mucho en Leapfrog. Mediante la implementación de este nuevo formato de modelo de bloques secundarios con la subdivisión octree, permitimos que nuestros usuarios mejoren la representación geométrica de los dominios de estimación y los modelos geológicos con un modelo de bloque informático más ligero, rápido y eficaz.
Mike Stewart, Technical Doman Expert at Seequent




